Skip to main content

RTL Design Engineer at Skyroot Aerospace

Hello, Dear Readers, Skyroot Aerospace has a vacancy for the RTL Design Engineer role. About Skyroot Aerospace: A cutting-edge startup founded by ex-ISRO scientists. Dedicated to affordable space access, we're rewriting aerospace technology rules. Our dynamic team fosters inventiveness, collaboration, and relentless excellence. Join us on a transformative journey to redefine space possibilities. Welcome to the forefront of space innovation with Skyroot Aerospace! Purpose of role: Understand architectural requirements and Design micro-architecture, implement design blocks using VHDL/Verilog for FPGA based Avionics packages for orbital launch vehicles and ground infrastructure. Job Requirements: 2+ Years of RTL and system design experience. Strong knowledge on Digital System Design (DSD). Strong knowledge of RTL/SoC design/integration with VHDL/Verilog. Strong knowledge in problem solving and debugging skills. Ability to understand architectural requirements and Design micro-archite...
Post a Comment

Verilog Code of Floating-Point Multiplier Design.

 Hello Dear Readers, 

Today in this post, I will provide some deep insight into the floating point multiplier. It's design, algorithms, and implementation using Verilog HDL languages.

First, let us understand what is IEEE Standard 754 Floating Point Numbers. 

The IEEE Standard for Floating-Point Arithmetic (IEEE 754) is a technical standard for floating-point computation which was established in 1985 by the Institute of Electrical and Electronics Engineers (IEEE). The standard addressed many problems found in the diverse floating point implementations that made them difficult to use reliably and reduced their portability. IEEE Standard 754 floating point is the most common representation today for real numbers on computers, including Intel-based PC’s, Macs, and most Unix platforms.

There are several ways to represent floating point number but IEEE 754 is the most efficient in most cases. IEEE 754 has 3 basic components:

  • The Sign of Mantissa – This is as simple as the name. 0 represents a positive number while 1 represents a negative number.
  • The Biased exponent – The exponent field needs to represent both positive and negative exponents. A bias is added to the actual exponent in order to get the stored exponent.
  • The Normalised Mantissa – The mantissa is part of a number in scientific notation or a floating-point number, consisting of its significant digits. Here we have only 2 digits, i.e. O and 1. So a normalised mantissa is one with only one 1 to the left of the decimal.

IEEE 754 numbers are divided into two based on the above three components: single precision and double precision.



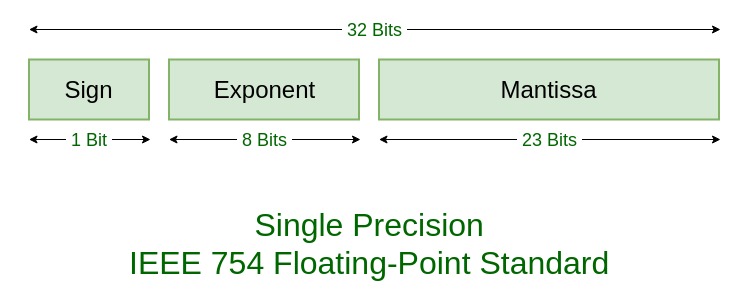
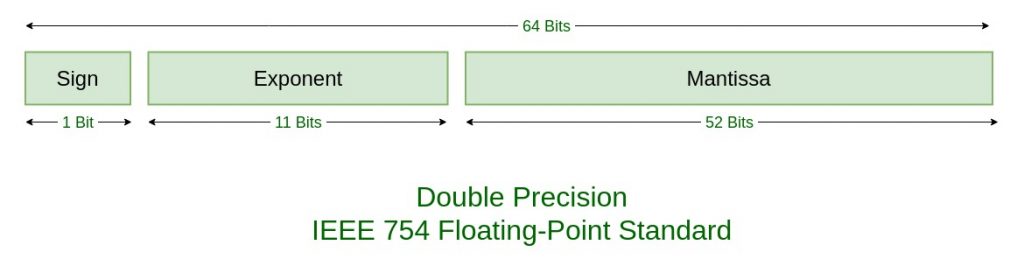
TYPESSIGNBIASED EXPONENTNORMALISED MANTISABIAS
Single precision1(31st bit)8(30-23)23(22-0)127
Double precision1(63rd bit)11(62-52)52(51-0)1023


Floating-point multipliers are crucial for handling arithmetic operations in various computational tasks. The floating-point multiplication algorithm can be complex, but here's a simplified breakdown:

Steps of Floating-Point Multiplication Algorithm

  1. Extract the Components:

    • Decompose the two floating-point numbers into their sign, exponent, and mantissa (fraction) components.

    • For IEEE 754 single precision:

      • Sign: 1 bit

      • Exponent: 8 bits

      • Mantissa: 23 bits (with an implicit leading 1)

  2. Compute the Result Sign:

    • The sign of the result is the XOR of the signs of the two operands.

    • If both signs are the same, the result is positive. If different, the result is negative.

  3. Add the Exponents:

    • Add the exponents of the two numbers.

    • Adjust the sum by subtracting the bias (127 for single precision) to account for the excess-127 representation.

  4. Multiply the Mantissas:

    • Multiply the mantissas (with the implicit leading 1).

    • This results in a product that is typically 48 bits for single precision (24-bit mantissa for each operand).

  5. Normalize the Result:

    • Check the most significant bit of the mantissa product. If it is 1, the product is already normalized.

    • If not, normalize the product by shifting it left and adjusting the exponent accordingly.

  6. Assemble the Result:

    • Combine the sign bit, the adjusted exponent, and the normalized mantissa to form the final floating-point result.

Example:

Let's work through an example to illustrate these steps.

Operands

  • A = 1.5 (in IEEE 754 single precision)

    • Binary: 0 01111111 10000000000000000000000

  • B = 2.0 (in IEEE 754 single precision)

    • Binary: 0 10000000 00000000000000000000000

Step-by-Step Calculation

  1. Extract Components:

    • A: Sign = 0, Exponent = 127, Mantissa = 1.10000000000000000000000

    • B: Sign = 0, Exponent = 128, Mantissa = 1.00000000000000000000000

  2. Compute Result Sign:

    • Result Sign = 0 XOR 0 = 0 (positive)

  3. Add Exponents:

    • Exponent Sum = 127 + 128 = 255

    • Adjusted Exponent = 255 - 127 = 128

  4. Multiply Mantissas:

    • Mantissa Product = 1.1 * 1.0 = 1.10000000000000000000000

    • Binary: 1.10000000000000000000000 (normalized)

  5. Normalize the Result:

    • The product is already normalized (most significant bit is 1).

    • Result Mantissa = 10000000000000000000000

    • Result Exponent = 128

  6. Assemble the Result:

    • Binary Result: 0 10000000 10000000000000000000000

    • Decimal Result: 3.0 (in IEEE 754 single precision)

Summary:

Floating-point multiplication involves:

  1. Extracting the sign, exponent, and mantissa.

  2. Calculating the result sign.

  3. Adding the exponents and adjusting for the bias.

  4. Multiplying the mantissa.

  5. Normalizing the result.

  6. Assembling the final result.


Let's dive into the Verilog code for a basic floating-point multiplier and explain each part in detail.

Verilog Code for Floating Point Multiplier:

module floating_point_multiplier (
    input  [31:0] a,      // 32-bit Floating point number a
    input  [31:0] b,      // 32-bit Floating point number b
    output [31:0] result  // 32-bit Floating point result
);

    // Decompose the inputs into sign, exponent, and mantissa
    wire sign_a = a[31];
    wire sign_b = b[31];
    wire [7:0] exponent_a = a[30:23];
    wire [7:0] exponent_b = b[30:23];
    wire [23:0] mantissa_a = {1'b1, a[22:0]};
    wire [23:0] mantissa_b = {1'b1, b[22:0]};

    // Calculate the result sign
    wire result_sign = sign_a ^ sign_b;

    // Add the exponents and adjust for the bias (127)
    wire [8:0] exponent_sum = exponent_a + exponent_b - 8'd127;

    // Multiply the mantissas
    wire [47:0] mantissa_product = mantissa_a * mantissa_b;

    // Normalize the result
    wire [22:0] result_mantissa;
    wire [7:0] result_exponent;
    if (mantissa_product[47]) begin
        // No need to shift mantissa
        result_mantissa = mantissa_product[46:24];
        result_exponent = exponent_sum + 1;
    end else begin
        // Normalize mantissa by shifting left
        result_mantissa = mantissa_product[45:23];
        result_exponent = exponent_sum;
    end

    // Combine the result
    assign result = {result_sign, result_exponent, result_mantissa};

endmodule

This Verilog code demonstrates a basic floating-point multiplier compliant with the IEEE 754 single precision standard. The code can be further optimized and extended to handle exceptions like underflow, overflow, and special values (e.g., NaN, infinity).



Comments

Post a Comment

Popular posts from this blog

Exploring the Role of LEF Files in VLSI Chip Design: A Beginner's Guide

Hello Dear Readers,   Today in this post, I will provide some deep insight into the LEF file role during the VLSI Chip Design process. In VLSI (Very Large Scale Integration) design, a LEF file is a file that contains information about the physical geometry of the standard cells used in a circuit. LEF stands for Library Exchange Format. A standard cell is a pre-designed logic cell that contains a specific function, such as a flip-flop or an AND gate. Standard cells are designed to be easily combinable and scalable to create more complex circuits. The physical geometry of each standard cell is defined in the LEF file. The LEF file contains information such as the width, height, and position of the pins and metal layers of each standard cell. It also contains information about the physical design rules that govern the placement of these cells on the chip. LEF files are important in VLSI design because they enable the interoperability of different design tools from different vend...
4 comments
Read more

Internship - SoC /IP Design at NXP India

Hello Dear Readers, Currently, at NXP India  vacancy for  Internship - SoC /IP Design   role.   We are looking for a Master degree student with Electronics and Communication Engineering, or related field, with an emphasis on SoC design. This is a full-time internship with a duration of about 11-12 months. Job Responsibility: Working with our experienced design team to design state of the art SoC hardware specific segment applications like Automotive, IoT, voice/object recognition, security, smart connectivity and touch sensing . Assisting experienced engineers with End-to-end ownership of SoC Design, Verification and implementation (Physical Design). Design and verify digital and Mixed-signal IPs. Document designs and present results. Job Qualification: Master student in electronic/computer engineering Creative and positive mindset Good knowledge on CMOS technologies Great communication skills, interpersonal skills, teamwork skills and can-do attitude Desire for a ca...
Post a Comment
Read more

IC Design Engineer at Broadcom

  Hello Dear Readers, Currently, at Broadcom vacancy for an IC Design Engineer role. Job Description: Candidate would be required to work on various phases of SOC physical design activities. The job will include but not limited to block level – floor-planning, partitioning, placement, clock tree synthesis, route, physical verification (LVS/DRC/ERC/Antenna etc). Should be able to meet congestion, timing and area metrics.  Candidate would be required to do equivalence checks, STA, Crosstalk delay analysis, noise analysis, power optimization. Should be able to implement timing and functional ECOs. Should have excellent problem-solving skill to help through congestion resolution and timing closure. Should have experience formal verification and timing analysis and ECO implementation. Experience with tools such as Innovus/Encounter, ICC, Caliber, LEC, Primetime etc is highly desirable. Candidate should be able to work independently and guide other team members. Should be ...
Post a Comment
Read more